Tagless final, First-class module, Modular implicit

はじめに

これは ML Advent Calendar 2017 の 19日目の記事です．

最近 Typed final (tagless-final) style を読みました。 このレクチャーノートではサンプルコードとして Haskell で型クラスを用いたものと OCaml でファンクターを用いたものが示されています。 このポストではそれらを OCaml の第一級モジュールと Modular implicit を使って書いてみました。 tagless final、第一級モジュール、Modular implicit それぞれについて真面目に説明するのは無理だったので簡単な説明にとどめています。

Final アプローチ

次のように代数的データ構造を定義してその上の処理を書くことがよくあると思います。

type exp = Lit of int | Neg of exp | Add of exp * exp

let rec eval = function
  | Lit i -> i
  | Neg e -> - (eval e)
  | Add (e1, e2) -> (eval e1) + (eval e2)

これに対して、コンストラクタを単に関数とすることで同じことが表現できます。

let lit i = i
let neg e = - e
let add e1 e2 = e1 + e2

前者のようにコンストラクタによって表現を埋め込む手法を initial アプローチ

後者のように関数によって表現を埋め込む手法を final アプローチ と呼びます。

しかし、上の final アプローチでは処理が複数ある場合明らかに困ったことになります。 例えば次の show のような処理を追加することを考えます。

let rec show = function
  | Lit i -> string_of_int i
  | Neg e -> "-" ^ (show e)
  | Add (e1, e2) -> "(" ^ (swho e1) ^ "+" ^ (show e2) ^ ")"

initial アプローチでは単に上の関数を追加するだけで良いのですが、 fianl アプローチでは同じ名前の別の関数を定義すること必要になるので工夫が必要です。

Haskellには型クラスがあるので次のように定義することができます。

class ExpSYM repr where
  lit : Int → repr
  neg : repr → repr
  add : repr → repr → repr

instance ExpSYM Int where 
  litn = n
  neg e = − e 
  add e1 e2 = e1 + e2

instance ExpSYM String where 
  lit n = show n
  neg e = "(-" + e + ")" 
  add e1 e2 = "(" + e1 + "+" + e2 + ")"

一方、OCaml ではモジュールとファンクターを使うことで解決することができます。 Haskell の型クラスをモジュール型、そのインスタンスをモジュールに対応させます。

module type ExpSYM = sig
  type repr
  val lit : int -> repr
  val neg : repr -> repr
  val add : repr -> repr -> repr  
end

module ExpSYMInt : ExpSYM with type repr = int = struct
  type repr = int
  let lit n = n
  let neg e = - e
  let add e1 e2 = e1 + e2
end

module ExpSYMString : ExpSYM with type repr = string = struct
  type repr = string
  let lit n = string_of_int n
  let neg e = "-" ^ e
  let add e1 e2 = "(" ^ e1 ^ "+" ^ e2 ^ ")"
end

repr は abstrac type として定義されているため、計算結果も抽象化されたままで普通に扱うことができなくなってしまうので、モジュールの定義時に with type 以下で実際の型の制約を入れています。

ファンクターを用いることで次のように使用できます。

utop # module F (M : ExpSYM) = struct 
        let tf = M.(add (lit 1) (neg (lit 2))) 
      end;;
module F : functor (M : ExpSYM) -> sig val tf : M.repr end

utop # let module M = F(ExpSYMInt) in M.tf;;
- : ExpSYMInt.repr = -1

utop # let module M = F(ExpSYMString) in M.tf;;
- : ExpSYMString.repr = "(1+-2)"

第一級モジュール

次に上の例を第一級モジュールを使って書き換えます。 第一級モジュールとはモジュールをコア言語内で扱うための機能で、これを用いれば 例えば関数の引数などにモジュールを渡すことが可能になります。

第一級モジュールについて詳しくは RWO などを参照してください。

上の例は次のように書き換えられます。

let tf1 (type a) (module M : ExpSYM with type repr = a) =
  M.(add (lit 8) (neg (add (lit 1) (lit 2))))

ExpSYM 内で abstract type として定義されている repr がエスケープしないように locally abstract type で注釈しています。

次のように使用できます。

top # tf1 (module ExpSYMInt);;
- : int = 5

utop # tf1 (module ExpSYMString);;
- : string = "(8+-(1+2))"

final アプローチの利点として、既存の部分に触れることなく表現を拡張できることがあります。

例えば、上の表現に mul を加えることを考えます。 initial アプローチではまず exp の定義に Mul of exp * exp を加え、eval、show もそれに合わせて書き換えることになります。一方 fianl アプローチでは次のコードを追加するだけで、既存の部分に手を加える必要はありません。

module type MulSYM = sig
  type repr
  val mul : repr -> repr -> repr
end

module MulSYMInt : MulSYM with type repr = int = struct
  type repr = int
  let mul e1 e2 = e1 * e2
end

module MulSYMString : MulSYM with type repr = string = struct
  type repr = string
  let mul e1 e2 = "(" ^ e1 ^ "*" ^ e2 ^ ")"
end

使用例は次の通りです。

let tfm1 (type a) (module S1 : ExpSYM with type repr = a) (module S2 : MulSYM with type repr = a) = 
  let open S1 in
  let open S2 in
  add (lit 7) (neg (mul (lit 1) (lit 2)))

utop # tfm1 (module ExpSYMInt) (module MulSYMInt);;
- : int = 5

utop # tfm1 (module ExpSYMString) (module MulSYMString);;
- : string = "(7+-(1*2))"

期待通りに動きますが、引数で渡す第一級モジュールが少し煩わしくなってきます。

Modular Implicit

上の例では第一級モジュールを引数に渡すことで処理をディスパッチしていました。 しかし、型からどう使われるかが分かればわざわざ引数として与えてやる必要がない気がします。 これを実現するのが Modular implicit という機能です。 Modular implicit が乗ったコンパイラは opam switch 4.02.0+modular-implicits で試せます。

Modular implicit を用いると上の例は次のように書けます。

module type ExpSYM = sig
  type repr
  val lit : int -> repr
  val neg : repr -> repr
  val add : repr -> repr -> repr  
end

implicit module ExpSYMInt : ExpSYM with type repr = int = struct
  type repr = int
  let lit n = n
  let neg e = - e
  let add e1 e2 = e1 + e2
end


implicit module ExpSYMString : ExpSYM with type repr = string = struct
  type repr = string
  let lit n = string_of_int n
  let neg e = "-" ^ e
  let add e1 e2 = "(" ^ e1 ^ "+" ^ e2 ^ ")"
end

let tf1 {S : ExpSYM} k =
let open S in
add (lit 8) (neg (add (lit 1) (lit 2)))
|> k

let eval : int -> int = fun x -> x
let show : string -> string = fun x -> x

第一級モジュールが来ていた位置の引数が波括弧に変わっています。 これは Modular implicit 用の構文で、この引数には型に合わせてコンパイラが選んだモジュールが暗黙に渡されます。その際 implicit をつけて定義したモジュールが候補になります。

また、型を合わせるためにその後の処理を継続の形で渡しています。

# tf1 eval;;
- : int = 5

# tf1 show;;
- : string = "(8+-(1+2))"

mul で拡張すると次のようになります。

module type MulSYM = sig
  type repr
  val mul : repr -> repr -> repr
end

implicit module MulSYMInt : MulSYM with type repr = int = struct
  type repr = int
  let mul e1 e2 = e1 * e2
end

implicit module MulSYMString : MulSYM with type repr = string = struct
  type repr = string
  let mul e1 e2 = "(" ^ e1 ^ "*" ^ e2 ^ ")"
end

let tfm1 (type a) {S1 : ExpSYM with type repr = a} {S2 : MulSYM with type repr = a} (k : a -> a) = 
  let open S1 in
  let open S2 in
  add (lit 7) (neg (mul (lit 1) (lit 2)))
  |> k

# tfm1 eval;;
- : int = 5
# tfm1 show;;
- : string = "(7+-(1*2))"

複数のモジュールを用いる際も引数としてそれぞれ渡す必要が無くなっています。

initial アプローチと final アプローチの関係

initial アプローチと final アプローチは互いに変換することも可能です。

type exp = Lit of int | Neg of exp | Add of exp * exp

implicit module ExpSYMExp : ExpSYM with type repr = exp = struct 
  type repr = exp
  let lit n = Lit n
  let neg e = Neg e
  let add e1 e2 = Add (e1, e2)
end

let initialize : exp -> exp = fun e -> e

let rec finalize : type a. {S : ExpSYM with type repr = a} -> exp -> a =
fun {S : ExpSYM with type repr = a} x ->
  let open S in match x with
    | Lit n -> lit n
    | Neg e -> neg (finalize e)
    | Add (e1, e2) -> add (finalize e1) (finalize e2)

let finalize : type a. {S : ExpSYM with type repr = a} -> (a -> a) -> exp -> a = fun {S : ExpSYM with type repr = a} f x ->
  let rec aux : type a. {S : ExpSYM with type repr = a} -> exp -> a =
    fun {S : ExpSYM with type repr = a} x ->
      let open S in match x with
        | Lit n -> lit n
        | Neg e -> neg (aux e)
        | Add (e1, e2) -> add (aux e1) (aux e2) in
  aux x |> f

# tf1 initialize;;
  - : exp = Add (Lit 8, Neg (Add (Lit 1, Lit 2))) 
# tf1 initialize |> (finalize eval);;
- : int = 5
# tf1 initialize |> (finalize show);;
- : string = "(8+-(1+2))"

Tagless Final

最後に　Tagless Final 形式での整数付きの STLC を書いてみます。

module type Symantics = sig
  type 'a repr
  val int : int -> int repr
  val add : int repr -> int repr -> int repr
  val lam : ('a repr -> 'b repr) -> ('a -> 'b) repr
  val app : ('a -> 'b) repr -> 'a repr -> 'b repr
end

type 'a r = R of 'a
let unR = function R x -> x

implicit module SymanticR : Symantics with type 'a repr = 'a r = struct
  type 'a repr = 'a r
  let int x = R x
  let add e1 e2 = R (unR e1 + unR e2)
  let lam f = R (fun x -> R x |> f |> unR)
  let app e1 e2 = R (unR e1 (unR e2))
end

type 'a s = S of (int -> string)
let unS = function S x -> x

implicit module SymanticS : Symantics with type 'a repr = 'a s = struct
  type 'a repr = 'a s
  let int x = S (fun _ -> string_of_int x)
  let add e1 e2 = S (fun h -> "(" ^ unS e1 h ^ "+" ^ unS e2 h ^ ")")
  let lam e = S (fun h -> let x = "x" ^ string_of_int h in
                          "("^x^" -> "^ (unS (e (S (fun _ ->x)))) (h+1) ^")")
  let app e1 e2 = S (fun h -> "(" ^ unS e1 h ^ " " ^ unS e2 h ^ ")")
end

let th1 {M : Symantics} f = 
  M.(app (lam (fun x -> add x x)) (int 21)) |> f

let eval = unR
let show x = unS x 0

# th1 eval;;
- : int = 42
# th1 show;;
- : string = "((x0 -> (x0+x0)) 21)"

型がつかない項が書けないことも確認できます。

# let th2 {M : Symantics} f = M.(app (int 4) (int 3)) |> f;;
Error: This expression has type int M.repr
       but an expression was expected of type ('a -> 'b) M.repr
       Type int is not compatible with type 'a -> 'b

まとめ

全体としてまとまり無く不親切な感じになりましたが、tagless final を modular implicit を使って書きました。

このポストでは触れていない部分を含めたコード全体は

ML Advend Clendar 2017 · GitHub

にあります。

参考

プログラミング言語 idris

これは Theorem Prover Advent Calendar 2016 17日目の記事として書かれました.

idrisは依存型を持つ純粋関数型プログラミング言語です. ちなみにアイコンはこんな感じ.

f:id:wkwkes:20161215155232p:plain *1

今月の初め, バージョン 0.99 がリリースされました. 機能もほぼ安定したといことで これを機に少し遊んでみたのでその紹介をします.

はじめに断っておきますが, 私自身 idris を触って間もないのでおかしなことを書いている可能性があります. 間違い等あれば指摘していただければ幸いです.

処理系

brew install idris などで降ってきます. idris でREPLが起動します.

$ idris
     ____    __     _
    /  _/___/ /____(_)____
    / // __  / ___/ / ___/     Version 0.99
  _/ // /_/ / /  / (__  )      http://www.idris-lang.org/
 /___/\__,_/_/  /_/____/       Type :? for help

Idris is free software with ABSOLUTELY NO WARRANTY.
For details type :warranty.
Idris>

ghciに近い感覚で使えます. 複数行入力は :let でできますが, やりにくいので一度ファイルにプログラムを記述してそれを読み込むのが無難だと思います. 実行ファイルが欲しければコマンドラインからidris -o hoge hoge.idr などとすればOKです.

基本構文

だいたい Haskell です. 型クラス相当のものやdo-notation まであります. 例えば 標準入力から受け取った文字列をそのまま出力するプログラムは次のように書けます.

main : IO ()
main = do x <- getLine
          putStrLn x

Haskellっぽいですね.

Haskell と違うところは Idris for Haskellers にまとまっていますが, すぐ気になるのは例えば

  • 評価が正格
  • : と :: が逆
  • 関数の型の記述が原則必須

などでしょうか.

また, 前述した通り idris には依存型があります.

たとえば伝統的な, 長さの情報をもつリストは次のように定義できます.

data Vect : Nat -> Type -> Type where
  Nil : Vect Z a
  (::) : a -> Vect k a -> Vect (S k) a

Vect 上の関数として例えば head を書いておきます.

head : Vect (S n) a  -> a
head (x :: _) = x

依存型・証明

依存型といえば Coq や Agda が有名ですが, 定理証明支援系としての側面の強いそれらに対して, idris は依存型を用いた(通常の)ソフトウェア開発の可能性を探ることを目標にしているそうです.

とは言っても依存型がある以上, 証明的なものを書く必要が出てきます. たとえば次の reverse 関数を考えます.

reverse : Vect n a -> Vect n a
reverse x = reverse_ x Nil
  where
    reverse_ : Vect n a -> Vect m a -> Vect (n + m) a
    reverse_ Nil ys = ys
    reverse_ (x :: xs) ys = reverse_ xs (x :: ys)

よさそうに見えますが, コンパイルすると怒られます.

When checking right hand side of Main.reverse, reverse_ with expected type
        Vect (S k + m) a

Type mismatch between
        Vect (k + S m) a (Type of Main.reverse, reverse_ a n x_shadow k (S m) xs (x :: ys))
and
        Vect (plus (S k) m) a (Expected type)

Specifically:
        Type mismatch between
                plus k (S m)
        and
                S (plus k m)

コンパイラはplus k (S m) と S (plus k m) が等しくないと言っています. 愛くるしいですね.

ここでplus k (S m) と S (plus k m) が等しいことを証明する必要がありますが, idris の証明はいくつか方法があります.

  • 示したいことを型にもつプログラムを直接書く.
    • 一番直接的な証明です. エディタのプラグインを使えば意外とシュッとかけます.
  • 対話的に証明する.
    • Coq のように対話的に証明を行えます. REPLから
      • :elab
      • :p

      のどちらかをタイプすることで対話環境に入ることができます. :elab は elaborator という idris に埋め込めるDSL的なもののスクリプトを生成します. :p も似たような証明のスクリプトを生成しますが現バージョンでは既に非推奨*2になっています.

証明のやり方がいくつかあって戸惑いますが, 少し触ってみたところ, 等式の証明をするときはプログラムを直接書くのがやりやすい. elaborator は構文が大げさで使いにくい. :p から入る証明モードが一番使いやすいと感じました. 遊んだ程度なので話半分に思ってください.

とりあえず plus k (S m) と S (plus k m) が等しいことを :elab で証明してみます. そのためにはまず証明する箇所をプログラム中に明示する必要があります.

reverse : Vect n a -> Vect n a
reverse x ?= reverse_ x Nil
  where
    reverse_ : Vect n a -> Vect m a -> Vect (n + m) a
    reverse_ Nil ys = ys
    reverse_ (x :: xs) ys ?= reverse_ xs (x :: ys)

?= に注意してください. これが証明する箇所を表します. 上のプログラムをREPLで実行すると

Idris> :l test.idr
Holes: Main.reverse_lemma_1, Main.reverse__lemma_1

となって, ?=に書き換えた証明すべきところが Holes になっています. idris では不完全な定義などが Holes として明示されます. REPLで :m とすれば Holes の一覧を見ることができます.

今から tactic を用いて Hole を埋めていくことになります.

まず Main.reverse_lemma_1 を埋めましょう. :elab コマンドで証明用のシェルに入ります.

*test> :elab Main.reverse_lemma_1


----------                 Goal:                  ----------
{hole0} : (a : Type) ->
          (n : Nat) -> Vect n a -> Vect (n + fromInteger 0) a -> Vect n a

Goal や 仮定 がでてきます.

tactic の詳細は :doc <tactic> を見てください. 一気にやります. 雰囲気を感じてもらえれば.

-Main.reverse_lemma_1> intro'

----------              Assumptions:              ----------
 a : Type
----------                 Goal:                  ----------
{hole0} : (n : Nat) -> Vect n a -> Vect (n + fromInteger 0) a -> Vect n a
-Main.reverse_lemma_1> intro'

----------              Assumptions:              ----------
 a : Type
 n : Nat
----------                 Goal:                  ----------
{hole0} : Vect n a -> Vect (n + fromInteger 0) a -> Vect n a
-Main.reverse_lemma_1> intro'

----------              Assumptions:              ----------
 a : Type
 n : Nat
 x : Vect n a
----------                 Goal:                  ----------
{hole0} : Vect (n + fromInteger 0) a -> Vect n a
-Main.reverse_lemma_1> compute

----------              Assumptions:              ----------
 a : Type
 n : Nat
 x : Vect n a
----------                 Goal:                  ----------
{hole0} : Vect (plus n 0) a -> Vect n a
-Main.reverse_lemma_1> rewriteWith `(plusZeroRightNeutral ~(Var `{{n}}))

----------              Assumptions:              ----------
 a : Type
 n : Nat
 x : Vect n a
----------                 Goal:                  ----------
{hole0} : Vect (plus n 0) a -> Vect (plus n 0) a
-Main.reverse_lemma_1> attack
----------              Other goals:              ----------
{hole0}
----------              Assumptions:              ----------
 a : Type
 n : Nat
 x : Vect n a
----------                 Goal:                  ----------
{hole1} : Vect (plus n 0) a -> Vect (plus n 0) a
-Main.reverse_lemma_1> intro'
----------              Other goals:              ----------
{hole0}
----------              Assumptions:              ----------
 a : Type
 n : Nat
 x : Vect n a
 value : Vect (plus n 0) a
----------                 Goal:                  ----------
{hole1} : Vect (plus n 0) a
-Main.reverse_lemma_1> fill (Var `{{value}})
----------              Other goals:              ----------
{hole0}
----------              Assumptions:              ----------
 a : Type
 n : Nat
 x : Vect n a
 value : Vect (plus n 0) a
----------                 Goal:                  ----------
{hole1} : Vect (plus n 0) a =?= value
-Main.reverse_lemma_1> solve

----------              Assumptions:              ----------
 a : Type
 n : Nat
 x : Vect n a
----------                 Goal:                  ----------
{hole0} : Vect (plus n 0) a -> Vect (plus n 0) a =?= \value => value
-Main.reverse_lemma_1> solve
reverse_lemma_1: No more goals.

証明が終わったら:qedコマンドで証明が出力されるのでそれをソースコードに貼り付ければ以降証明の必要はありません.

-Main.reverse_lemma_1> :qed
Proof completed!
Main.reverse_lemma_1 = %runElab (do intro'
                                    intro'
                                    intro'
                                    compute
                                    rewriteWith `(plusZeroRightNeutral ~(Var `{{n}}))
                                    attack
                                    intro'
                                    fill (Var `{{value}})
                                    solve
                                    solve)

Main.reverse__lemma_1 も同じ要領でやった結果ソースコードは次のようになります.

reverse : {n: Nat} -> Vect n a -> Vect n a
reverse x ?= reverse_ x Nil
  where
    reverse_ : {n: Nat} -> {m: Nat} -> Vect n a -> Vect m a -> Vect (n + m) a
    reverse_ Nil ys = ys
    reverse_ (x :: xs) ys ?= reverse_ xs (x :: ys)

Main.reverse_lemma_1 = %runElab (do intro'
                                    intro'
                                    intro'
                                    compute
                                    rewriteWith `(plusZeroRightNeutral ~(Var `{{n}}))
                                    attack
                                    intro'
                                    fill (Var `{{value}})
                                    solve
                                    solve)

Main.reverse__lemma_1 = %runElab (do intro'
                                     intro'
                                     intro'
                                     intro'
                                     intro'
                                     intro'
                                     intro'
                                     intro'
                                     compute
                                     rewriteWith `(plusSuccRightSucc ~(Var `{{k}}) ~(Var `{{m}}))
                                     attack
                                     intro'
                                     fill (Var `{{value}})
                                     solve
                                     solve)

型が通るのが確認できます.

Idris> :l test.idr
*test>

以上が :elab による証明の例でした.

対話的証明ではなく直接プログラムを書くスタイルのプログラム例も書いておきます.

とりあえず Reading HoTT in Coq の Coq のプログラムを参考に id : A -> A が A の間の equivalence になることを示してみました. (余分な関数も含まれています)

なお, 等式の証明についての詳しい説明は The Idris Tutorial: Thorem Proving などにあります.

total
inverse : {A: Type} -> {x, y: A} -> (x = y) -> (y = x)
inverse Refl = Refl

total
concat : {A: Type} -> {x, y: A} -> {z: A} -> (x = y) -> (y = z) -> (x = z)
concat Refl Refl = Refl

total
concat_p1 : (A: Type) -> (x: A) -> (y: A) -> (p: x = y) -> (concat p Refl = Refl{x = x})
concat_p1 A x x Refl = Refl{x = (Refl{x = x})} 

total
inv_inv : {A: Type} -> {x, y: A} -> (p: x = y) -> (inverse (inverse p)) = p
inv_inv Refl = Refl

total
concat_assoc : (A: Type) -> (x: A) -> (y: A) -> (z: A) -> (w: A) -> (p: x = y) -> (q: y = z) -> (r: z = w) -> ((concat p (concat q r)) = (concat (concat p q) r))
concat_assoc A x x x x Refl Refl Refl = Refl

total
transport : {A: Type} -> {x, y: A} -> (P: A -> Type) -> (p: x = y) -> (u: P x) -> (P y)
transport P Refl u = u

total
ap : {A, B: Type} -> {x, y: A} -> (f: A -> B) -> (p: x = y) -> (f x = f y) 
ap f Refl = Refl

total
apD : {A: Type} -> {B: A -> Type} -> {x, y: A} -> (f: (a: A) -> B a) -> (p: x = y) -> transport _ p (f x) = f y
apD f Refl = Refl

total
sect : {A, B: Type} -> (A -> B) -> (B -> A) -> A -> Type
sect s r x = r (s x) = x

record IsEquiv (A: Type) (B: Type) (f: A -> B) where
  constructor BuildIsEquiv
  equiv_inv : B -> A
  eisretr : (x: B) -> sect equiv_inv f x
  eissect : (x: A) -> sect f equiv_inv x
  eisadj : (x: A) -> eisretr (f x) = ap f (eissect x)

record Equiv (A: Type) (B: Type) where
  constructor BuildEquiv
  equiv_fun: A -> B
  equiv_isequiv: IsEquiv A B equiv_fun

total
idmap : (A: Type) -> A -> A
idmap A = \ x : A => x

isequiv_idmap : (A: Type) -> IsEquiv A A (idmap A)
isequiv_idmap A = BuildIsEquiv (idmap A) (\ _ : A => Refl) (\ _ : A => Refl) (\ _ : A => Refl)

equiv_idmap : (A: Type) -> Equiv A A
equiv_idmap A = BuildEquiv (idmap A) (isequiv_idmap A)

concat_p1 の Refl の型が推論してもらえず少し手こずりましたが, 他はすんなりいったと思います.

その他の話題

バックエンドがいろいろある

バックエンドというよりコンパイルのターゲットという方がいいかもしれません. Language Reference: Code Generation Targets にまとまっています. ここにも書き写しておきます.

Malfunction を経由して OCaml のバックエンドを利用する話は少し話題になっていた記憶があります.

エディタ

emacs, vim , atom あたりにはプラグインがあります. 型を書くとその実装の雛形を生成してくれたり, 簡単な証明を探索してくれたりして便利です. 詳しい説明は Theorem Proving: Pattern Matching Proofs にあります.

ちなみに私は emacs の idirs-mode を使いました.

おわりに

プログラミング言語の紹介と言いながら構文にほぼ言及しないなどよくわからない記事になりましたが, 参考になれば幸いです.

最後に参考にした・参考になりそうなページをあげて終わります.

*1: https://github.com/idris-lang/Idris-dev/blob/master/icons/idris-128x128.png　

*2:この辺りに経緯が Replacing the former tactic system with elaborator reflection

LLVMのOCaml bindingをためす

前からLLMVが気になっていて, きつねさんの本 をざっと読んだりしたが手を動かしてなかったのでチュートリアルをやることにした.

LLVM Tutorial: Table of Contents — LLVM 3.8 documentation

古いチュートリアルだということは知っていたが他にないので仕方なくやってみた.*1

現在の環境(LLVM3.8)でやるのは厳しかった. 途中までだがせっかくなのでメモしておく.

好みでC++ではなくOCamlを選んだ.

LLVMはC++で書かれているがOCamlのbindingが公式でサポートされている. 雑に検索したところOCaml以外にHaskell, Go, Rustなどにもbindingがあるらしい.

そういえばRustの初期のコンパイラはOCamlとLLVMで作られていたみたいな話があった気がする.

コード

ビルドするにはLLVM(3.8)とOCamlの各種ライブラリ(llvm, ctypes, (ppx_deriving))とocamlbuildが必要. 4章の分までは一応動くが後で述べるように色々問題がある.

github.com

やったこと

1章・2章

字句解析と構文解析で, 特にLLVMに関係がない.

構文解析, 字句解析ともにCamlp4をバリバリ使っているけど, 今はppxが推奨されるらしいのでどうなのかという気がする.

私はocamllexとmenhirを使った.

3章

ここからLLVMを使う.

3章では抽象構文木からLLVM IRという中間コード生成をする. そのままコンパイルしようとするとaddやmulでdoubleを使ってることを怒られる. faddやfmulに書き換えてdoubleをfloatにするとコンパイルできる.

4章

最適化のためにパスをいくつか入れて, そのあとJITで動かす.

4章のコードをビルドしようとすると

Error: Unbound module ExecutionEngine

になる. ググると同じエラーが出てる人が多い.

3.8にはそもそもLlvm_executionengine.ExecutionEngineなるモジュールがない. 3.5まではあるみたいなので, LLVMのバージョン3.6のリリースノート を見ると

LLVM 3.5 has, unfortunately, shipped a broken Llvm_executionengine implementation. In LLVM 3.6, the bindings now fully support MCJIT, however the interface is reworked from scratch using ctypes and is not backwards compatible.

ということらしい.

パスはとりあえず諦めてJITで動かすことを目標にした. 名前と型とモジュールの説明からそれっぽい関数を探して書き換えていくと一応動いた.

# 1 + 1;                                                                                                                            
                                                                                                                                    
define float @"00"() {                                                                                                              
entry:                                                                                                                              
  ret float 2.000000e+00                                                                                                            
}                                                                                                                                   
                                                                                                                                    
Evaluated to 2. 
# def foo(a b) a*a + 2*a*b + b*b;                                                                                                   
                                                                                                                                    
define float @foo(float %a, float %b) {                                                                                             
entry:                                                                                                                              
  %fmultmp = fmul float %a, %a                                                                                                      
  %fmultmp1 = fmul float 2.000000e+00, %a                                                                                           
  %fmultmp2 = fmul float %fmultmp1, %b                                                                                              
  %faddtmp = fadd float %fmultmp, %fmultmp2                                                                                         
  %fmultmp3 = fmul float %b, %b                                                                                                     
  %faddtmp4 = fadd float %faddtmp, %fmultmp3                                                                                        
  ret float %faddtmp4                                                                                                               
}                                                                                                                                   
                                                                                                                                    
                                                                                                                                    
# foo(2,3);                                                                                                                         
                                                                                                                                    
define float @"00"() {                                                                                                              
entry:                                                                                                                              
  %calltmp = call float @foo(float 2.000000e+00, float 3.000000e+00)                                                                
  ret float %calltmp                                                                                                                
}                                                                                                                                   
                                                                                                                                    
Evaluated to 25.

それでもまだ色々問題がある

  • 無名関数が実行できない(チュートリアル通り無名関数の名前を""にしてるとexception Llvm_executionengine.Error("Function not found")になる
  • トップレベルのexpressionの評価が一度しか行えない(二度目はエラーになる)
  • extern cosなどで宣言した関数が正しく動かない

とりあえず無名関数にも内部では名前("00")をつけたり, 一度トップレベルのexpressionを評価するたびにllmoduleを作り直したりすることでそれっぽい挙動にはなるが, 評価のたびに関数の定義が消えるというような他の問題が生じる.

5章以降では構文も増えてこのまま進むのは無理そうなので一旦OCamlを離れてC++でLLVMを知るのが先だなという気持ちになってきた.

感想

OCamlだけでLLVMを始めるのは厳しい

その他

構文解析木をプリントするのに初めてppx_derivingを使ってみたら便利だった. 今まで書いてきた手書きプリンターはなんだったのか.

# def foo(a b c) (a - b) * (b - c) + (c - a);   
                                                                                    
(Ast.Def                                                                                                                            
   Ast.Function (Ast.Prototype ("foo", [|"a"; "b"; "c"|]),                                                                          
     Ast.Binary_c ("+",                                                                                                             
       Ast.Binary_c ("*",                                                                                                           
         Ast.Binary_c ("-", (Ast.Variable "a"), (Ast.Variable "b")),                                                                
         Ast.Binary_c ("-", (Ast.Variable "b"), (Ast.Variable "c"))),                                                               
       Ast.Binary_c ("-", (Ast.Variable "c"), (Ast.Variable "a")))))

参考にしたもの

*1:この段階で古かったようなので相当 OCaml で LLVM -- 事始め - Oh, you `re no (fun _ → more)

ラムダ計算の評価器とBöhm tree

気持ち

『きつねさんでもわかるLLVM』を読んだので何か書いてみようと思い, 一回書いておくかというのもあってラムダ計算の評価器を書くことにしました. 書いた結果, LLVMを使っても仕方ないことに気がついた(遅い！) のでLLVMはつかっていません. ついでにBöhm treeを出力させることにしました.

Böhm tree

ググると詳しく解説したPDFなどが見つかるので簡単に書きます.

任意のラムダ項は

  1. { \displaystyle \lambda x_0 . \cdots \lambda x_n . x M_0 M_1 \cdots M_m \ \ (n, m \geq 0) }
  2. { \displaystyle \lambda x_0 . \cdots \lambda x_n . (\lambda x M) M_0 \cdots M_m \ \ (n \geq 0 , m \geq 0) }

のどちらかの形にかけます*1. 1 を頭正規形といい, 2 の{ \displaystyle (\lambda x M) M_0}という部分を頭基といい, 頭基をβ簡約することを頭変換といいます. あるラムダ項が頭正規形をもつなら頭変換だけで頭正規形に変換できることが知られています.

これらの性質を使ってラムダ項を木として表現したものをBöhm tree といいます. 以下が定義です.

ラムダ項{M}が

  • 頭正規形の形のとき, BT({M}) = 親 : { \displaystyle \lambda x_0 . \cdots \lambda x_n . x }, 子 : BT({M_0}), {\cdots}, BT({M_m})

  • 2の形のとき, 頭正規形になるまで頭変換を繰り返します. 頭正規形にならないときは無限木は書いていられないので BT({M}) {= \bot}とします.

これらを繰り返すことで得られる木がBöhm treeです.

コード

出力の形式をどうするか考えましたが, 手軽さと, ひょっとしていつか使えるかもしれないと思い{\displaystyle \LaTeX}のコードとして出力することにしました. 木を表示には tikz-qtree*2というパッケージをつかいました.*3.

C++で書きました. 良いC++書き方がわからないので変なことをしている可能性があります. 定義通りではないのですが, 正規形があるかわからない場合はある程度繰り返して止まるようになっています.

github.com

例

出力された{\displaystyle \LaTeX}のコードから出力された結果です. 入力とともに出力されています.

f:id:wkwkes:20160309221223p:plainf:id:wkwkes:20160309221230p:plainf:id:wkwkes:20160309221236p:plainf:id:wkwkes:20160309221242p:plainf:id:wkwkes:20160309221249p:plain

参考にした本

Amazon CAPTCHA

字句解析器・構文解析器, ASTの設計を参考にしました.

Amazon CAPTCHA

De Brujinインデックスのあたりを参考にしました.

Amazon CAPTCHA

http://pauillac.inria.fr/~levy/courses/tsinghua/lambda/3-5/lecture3-5-4.pdf

Böhm treeの参考にしました.

*1:ここで帰納法が回る

*2:CTAN: Package tikz-qtree

*3:パッケージの仕様上あまり深い木は出力できないみたいです

Billiard-ball computer

Billiard-ball Computerという計算モデルがあると知った。
Billiard-ball computer - Wikipedia, the free encyclopedia
ボールの存在で1と0をあらわし、うまく衝突させることで論理回路を作るというものである。チューリング完全性があるらしい。

具体的には、摩擦がなく完全弾性衝突するという条件下で、二つのボールを入力とみなせば、以下のような衝突でANDを構成することができる。
f:id:wkwkes:20150719021709p:plain

あと、NOTがほしいが、これらはANDほど単純には構成できない。
Conservative logic - Springerを見るとFredkin gateと呼ばれる回路を使えばいいらしい。

そのためにまず、Switch gateと呼ばれる以下の回路を考える。*1
f:id:wkwkes:20150719021925p:plain

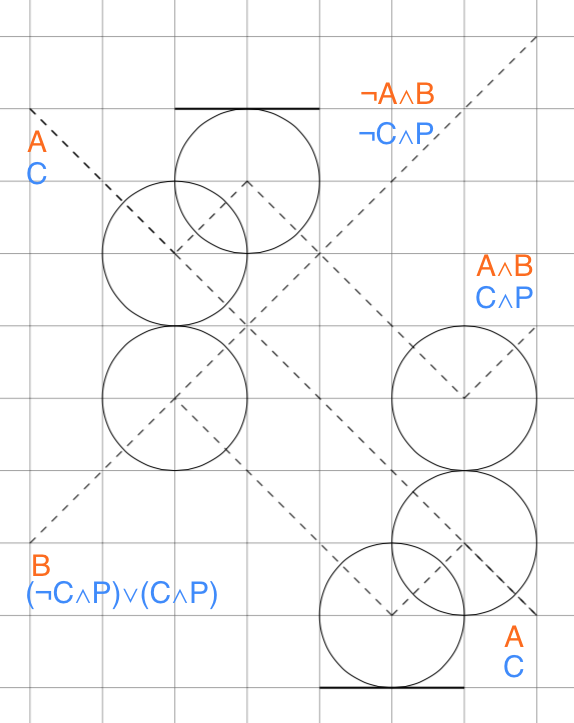
左から入力し、右へ出力する時をオレンジで、右から入力し、左へ出力する時を青で表した。

これを4つ用いると以下のようにFredkin gateが構成出来る。
f:id:wkwkes:20150720212255p:plain

代入すると確かめられるが、Fredkin gateの真ん中の出力は、

  • Q=0 のとき (C\wedge P) \vee (\neg C \wedge Q) = C \wedge P
  • P=0 かつ Q = 1のとき (C\wedge P) \vee (\neg C \wedge Q) = \neg C

などとなる。
2つ目の性質からNOTが得られる。

以上でANDとNOTが構成できたので、Billiard-ball Computerがチューリング完全であることが確かめられた。

3DCGを作る環境があったので以上のこと使って、NOTとXORをCGでシミュレートしようと試みた。

物理演算でやろうとしたところ、回路が長くなるとどうしても思い通りの挙動を取らなかったため、シミュレーションは諦めて、理想上のモデルの動く様子を動画にした。

それぞれNOTに対して、1と0を入力した様子を表す。

Fredkin gate を4つ合わせて作ったXORに1と0を入力した様子を表す。レンダリングのミスで見にくいが、たしかに1を出力している。

*1:Switch gateとFredkin gateの構成は一例にすぎず、同じ挙動をとればどんな構成でもいいみたい。