Billiard-ball computer
Billiard-ball Computerという計算モデルがあると知った。
Billiard-ball computer - Wikipedia, the free encyclopedia
ボールの存在で1と0をあらわし、うまく衝突させることで論理回路を作るというものである。チューリング完全性があるらしい。
具体的には、摩擦がなく完全弾性衝突するという条件下で、二つのボールを入力とみなせば、以下のような衝突でANDを構成することができる。

あと、NOTがほしいが、これらはANDほど単純には構成できない。
Conservative logic - Springerを見るとFredkin gateと呼ばれる回路を使えばいいらしい。
そのためにまず、Switch gateと呼ばれる以下の回路を考える。*1
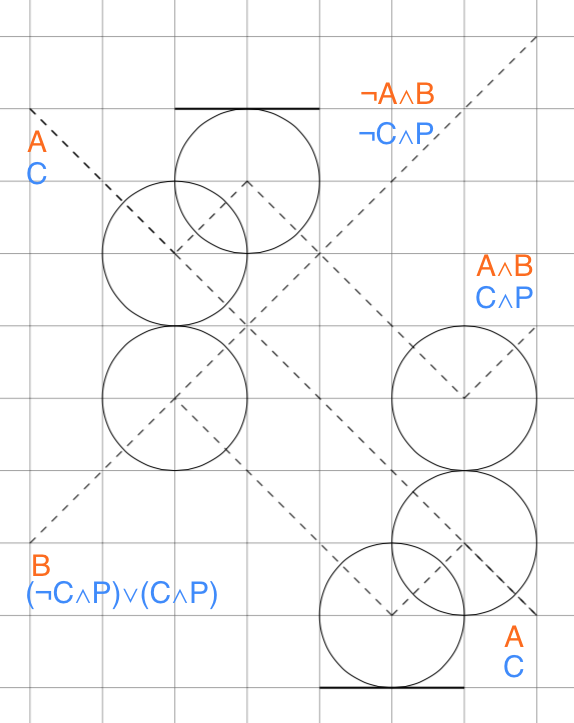
左から入力し、右へ出力する時をオレンジで、右から入力し、左へ出力する時を青で表した。
これを4つ用いると以下のようにFredkin gateが構成出来る。

代入すると確かめられるが、Fredkin gateの真ん中の出力は、
のとき
かつ
のとき
などとなる。
2つ目の性質からNOTが得られる。
以上でANDとNOTが構成できたので、Billiard-ball Computerがチューリング完全であることが確かめられた。
3DCGを作る環境があったので以上のこと使って、NOTとXORをCGでシミュレートしようと試みた。
物理演算でやろうとしたところ、回路が長くなるとどうしても思い通りの挙動を取らなかったため、シミュレーションは諦めて、理想上のモデルの動く様子を動画にした。
それぞれNOTに対して、1と0を入力した様子を表す。
Fredkin gate を4つ合わせて作ったXORに1と0を入力した様子を表す。レンダリングのミスで見にくいが、たしかに1を出力している。
*1:Switch gateとFredkin gateの構成は一例にすぎず、同じ挙動をとればどんな構成でもいいみたい。